A Mathematical Postscript

Below we see examples of the modified version of Walsh’s formula applied to the case of the 2 Livingston men, whose most recent shared paternal ancestor was according to genealogy Philip Livingston (1686-1749), and to the case the contemporary Plantagenets and Richard III, whose most recent shared paternal ancestor was according to genealogy Edward III (1312-1377).

Philip Livingston (1686-1749):

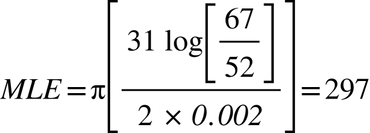
Edward III (1312-1377)

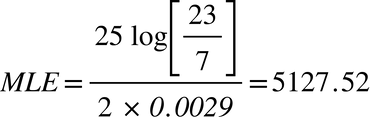
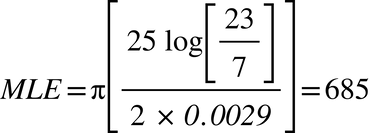
In both these cases, the modified form of Walsh’s formula identifies the TMRCA more or less perfectly, but it is evident that a more sophisticated formula is required. 

As means of arriving at such a formula, consider that we can simulate Pi[x] by using the function:

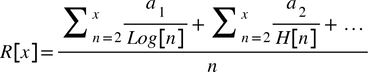
From another point of view on this same process, we see that dividing Pi[x] by the simulating function (or vice versa) results in a set of waves that oscillate around unity and decay over time: 

It follows that the primes are wave-like. Since the primes are the multiplicative atoms of the number line, this gives rise to the idea that the number line -and all lines- are wave-like, and to some extent dis-uniform. I would argue that flatness and unity are illusions, but that coherence is preserved by the strict limits on the extent of the curvature and dis-uniformity given by the Riemann Hypothesis (RH)... 

Anyway, from the idea of the wave-like/dis-uniform nature of genetic lines comes the following formula for identifying the TMRCA of the Y-chromosomes of a pair of individuals:

From here, we can input any proposed relationship between the haplotypes of these individuals, any number of matched and mismatched markers, together with a precisely defined TMRCA (e.g. 1686-1749 or 1322-1375), and let the coefficients a1 and a2 vary accordingly. 

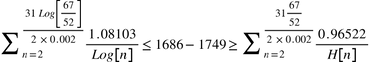
Then we slot these sums into R[x] and consider the fit:

In this way, then, the genealogical question of who begat whom is turned into a purely mathematical question. The point is, not so much to get an accurate formula for the TMRCA, as it is to get an accurate mathematical model of genetic change.

Every professional geneticist -and everyone with any acquaintanceship with an genetics- will scoff at the proposal that it is possible to get from -say- G to R in any amount of time, since R isn't even an off-shoot of the G-branch of the Y-DNA tree, but this attitude rests on the deep-lying ancient assumption that lines are flat and uniform (which is equivalent to the assumption that genetic mutations occur at a constant rate and in a forwards direction.) Wavy, dis-uniform lines (genetic mutations that slow down over time and occur in both a forwards and a backwards direction), totally change the basic structure of the tree, and make such transitions, not merely possible, but commonplace.

Squaring these waves into bell curves, we see that in the earlier stages of an arithmetic progression, the probability of departures from uniformity is greater, and that as the progression continues, this probability diminishes. Grasp this simple idea, apply it, and many of the numerous conflicts there are between genetics and genealogy can be resolved.