A New Idea

As indicated, there are two kinds of genealogical DNA tests. One kind relies on the fact that Y-DNA, passed down from father to son, and Mitochondrial DNA passed down from mother to child, do not recombine, which allows for the tracing of paternal and maternal lines. The other kind of test looks at all the chromosomes for shared recombinant DNA. With every generation that passes, approximately 1/2 of one’s DNA is lost: a child has 1/2 the DNA of their parent, a grandchild has 1/4, a great grandchild 1/8 and so on and so on. By looking at their amount of shared DNA it can theoretically be deduced how many generations ago the most recent common ancestor of two people lived.

We turn now to an observation I made about the shared DNA between myself and my African-American cousins: on the plausible assumption that some or all of these matches are due to shared Livingston ancestry, the most recent common ancestors are further back than expected... All of my many African-American cousins, with a single possible exception, are predicted by the percentage of shared DNA to be 4th - 5th cousins. But if they are Livingston descendants, then at closest, they are 8th cousins (James Livingston had offspring in both Monaghan and the US).

A possible solution to the problem -and something I have been pondering for over a decade- is as follows... Every family tree is associated with the line

• 1=1 (self)
• 1/2+1/2 =1 (parents)
• 1/4+1/4+1/4+1/4 =1 (grandparents)
• 1/8+1/8+1/8+1/8+1/8+1/8+1/8+1/8+1/8 =1 (great grandparents)...

Part of this tree -the father’s sub-line and the mother’s sub-line- involves the transmission of non-recombinant DNA, while every other sub-line involves the transmission of recombinant DNA. If we count only the unique nodes in a family tree (the number of unique ancestors), this line will be shorter or longer, depending on the number of non-unique nodes. When a tree involves a greater than average number of non-unique nodes, the line will be shorter than average. Rev. John Livingston's partial family tree illustrates what I mean (the recurring names are emboldened):

1st Generation

Rev. John Livingstone (c1603-c1673)

2nd Generation

William Livingstone (c1576-c1641)

Agnes Livingstone (c1575/85-c1617)

3rd Generation

James Livingstone (-c1547)

Alexander Livingstone (-c1564)

Barbara Forrester

Thomas Livingstone (-c1560)

4th Generation

William Livingstone (-c1514)

Agnes Hepburn

William Livingstone (-c1514)

Janet Bruce (-c1545)

Alexander Livingstone

Elizabeth Hepburn

Alexander Menteith…

There are a number of recurrent ancestors early on, but by the time we get to the 22nd generation we find many recurrent ancestors:

Ethelred II the Unready (–1016)

Alfflaed ----- 

Uhtred of Bamburgh (–c1016)

Ecgfrida of Durham 

Baldwin II of Boulogne (c0990–c1033)

Adelina of Holland (c0990–c1045)

Lambert I, Count of Louvain (c0950–1015)

Gerberga of Lower Lorraine 

Richard II of Normandy (c0975–1027)

Judith of Brittany (c0982–1017)

Fulbert of Falaise 

Hugh Capet (c0938–0996)

Adelaide of Aquitaine (–c1004)

William I of Provence 

Adelaide of Anjou (c0947–1026)

Vladimir Svyatoslavich (c0958–1015)

Rognilda ----- 

Olof Skotkonung (c0980–c1022)

Estrid of the Obotrites (c0979–1035)

Herbert III of Vermandois (c0955–c0993)

Ermengard of Bar-sur-Seine (0946–c1035)

Robert I of Normandy (c1004–1035)

Herleve of Falaise (c1003–c1050)

Baudoin V of Flanders (c1012–1067)

Adela of France (c1009–1079) 

Roger de Montgomerie 

Geoffrey of Brionne 

Osbern Giffard (c1020–c1085)

Aveline de Crepon 

Gerard Flaitel 

Ebles of Roucy 

Beatrix of Hainault 

Richard II of Normandy (c0975–1027)

Judith of Brittany (c0982–1017) 

Fulbert of Falaise

Baudoin IV of Flanders (c0980–1035)

Ogive of Luxembourg (–1030)

Robert II, King of France (0972–1031)

Constance of Arles (c0986–1034)

Robert II, King of France (0972–1031)

Constance of Arles (c0986–1034)

Yaroslav I the Wise (c0978–1054)

Ingegerd Olofsdotter (1001–1050)

Otho of Vermandois (0979–1045)

Parvia ----- (c0990–)

Raoul III of Valois

Adele de Bar-sur-Aube

Geoffrey of Brionne

Osbern Giffard (c1020–c1085)

Aveline de Crepon

Gerard Flaitel

Ebles of Roucy

Beatrix of Hainault

Robert II, King of France (0972–1031)

Constance of Arles (c0986–1034)

Yaroslav I the Wise (c0978–1054)

Ingegerd Olofsdotter (1001–1050)

Otho of Vermandois (0979–1045)

Parvia ----- (c0990–)

Raoul III of Valois

Adele de Bar-sur-Aube

Malcolm III of Scotland (1031–1093)

St. Margaret of Scotland (c1045–1093)

Waltheof II of Northumbria (c1050–1076)

Judith of Lens (c1054–c1086)

William de Warenne

Gundred ----- 

Hugh I of Vermandois (c1057–1101)

Adéle of Vermandois (c1062–c1124)

Ranulf III le Meschin (–1129)

Lucy of Bolingbroke (–c1138)

Robert of Gloucester (c1090–1147)

Mabel FitzHamon (c1090–1157)

Gilbert Fitzrichard de Clare (c1066–c1115)

Adeliza de Clermont-en-Beauvaisis

Ranulf III le Meschin (–1129)

Lucy of Bolingbroke (–c1138)

Henry I, King of England (c1068–1135)

Robert FitzHamon (–1107)

Sibyl de Montgomerie

Robert de Beaumont (c1049–1118)

Isabel de Vermandois (c1081–1131)

Ralph de Waer (Gael) (c1042–c1096)

Gilbert Fitzrichard de Clare (c1066–c1115)

Adeliza de Clermont-en-Beauvaisis

Robert de Beaumont (c1049–1118)

Isabel de Vermandois (c1081–1131)

Enna MacMurrough

Muitchertach O'Toole 

Cacht Inion Loigsig O'Morda

A shorter line, we know from number theory, involves a greater number of prime numbers (non-recombinant), and a lessor number of composites (recombinant). The primes thin out with arithmetic increase, while composites thicken up. So it may be hypothesised that the shorter and more prime-dense a genetic line, the faster the average mutation rate of non-recombinant DNA. 

Let n be the number of STR markers, let k be the number of matching markers, let m be the mutation rate, and the most likely estimate (MLE) back to the time of the most recent common ancestor (TMRCA) is -by Bruce Walsh’s formula- log n over k, over 2 m. This is the formula used earlier to arrive at a date in the late 1600s as the MLE/TMRCA of my uncle and his Livingston Big-Y match. These men match 107 out of 111 markers, and using this information, and a mutation rate of 0.0029, the formula gives a binomial distribution curve that peaks around 11 generations ago: 

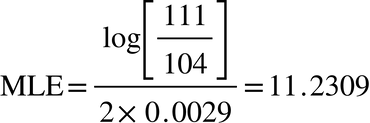
This may or may not be right -it is at least historically plausible- but the fact that the formula often produces results that are wildly inaccurate can be demonstrated by running it on my uncle's non-Livingston 111 marker matches. The shared ancestors in these cases lived before the era of surnames, and in the case of the Scandinavians, 1000s of years ago, and yet the same formula using the same numbers yields TMRCAs in the 17th century. Here for example is what we get for the Norwegian Silvertson:

As it stands, Walsh's formula is a very blunt tool indeed, but with the use of some number analytic theory, it can be modified according to the length and prime-density of a line to allow for faster or slower mutation rates, and for mutation rates that follow rough curves rather than straight lines. 

A simple example of what I mean can be given using genealogical and genetic data drawn from the Livingston/MacLea Y-DNA Project... A Robert H Livingston has a family tree connecting him to Robert Livingston (1654-1728), the son of Rev John Livingston. Another Livingston man—either John Preston Livingston (1917-2009) or a first cousin—is 

...said to descend from the Livingstons of Clermont via two sons of "Robert of Clermont", 3rd lord of the manor, Robert "Cambridge" Livingston (line carrying the Livingston paternal DNA), and John "of Oak Hill" Livingston (through two of his grand-daughters). The great-grandfather of the participant was Col. Charles Edward Livingston of Red Hook, New York, who served with the Union N.Y. 76th Infantry Volunteers during the American Civil War. He was the son of Robert Francis Livingston, a Surveyor and Civil Engineer, who, in turn, was the son of Robert Swift Livingston. Robert Swift Livingston was the son of Robert "Cambridge" Livingston and Alice Swift.

The most recent common ancestor of the two men is Philip Livingston (1686-1749):

They share 52 of 67 markers, and so by Walsh's formula, a generation length of 31, and a mutation rate of 0.002, this gives us a MLE/TMRCA of 1964 years ago.

They share 52 of 67 markers, and so by Walsh's formula, a generation length of 31, and a mutation rate of 0.002, this gives us a MLE/TMRCA of 1964 years ago.

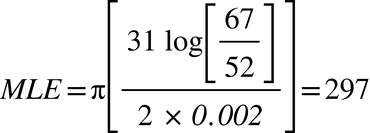
We have by these means effectively changed the mutation rate from 0.002 to 0.0132271. The basic idea is that, since the primes thin out over time, the revised formula involves mutation rates that decrease as a line grows longer. Because the distribution of the primes is erratic, this decrease is rough rather than smooth. This allows for mutation rates that are exceptionally fast, and for the random appearance of Y-DNA results that—against the background assumption that mutations are uniform and smooth—appear anomalous. The modified formula is in its present form bound to deliver inaccurate predictions, but there is a way to refine it to contend with this and with every other scenario (I will present this as straightforwardly as I can in a mathematical postscript). 

The shorter and more prime-dense the line, the more likely it is that the mutation rates of non-recombinant DNA will be faster and more erratic than expected; and the shorter and more prime-dense the line, the more likely it is that the mutation rates of recombinant DNA will be slower and less erratic than expected. In the first case, the most recent common ancestors will tend to be closer in time than expected; in the second case, the most recent common ancestors will tend to be further back in time than expected. Inevitably, prime-dense lines have a tendency to impose their genetics on the less prime-dense lines with which they come into contact.